Convolutional neural networks introduced by Yann lacunae in 1998 and used in so many applications today from image classification to audio synthesis and wavenet convolutional neural networks is one of those phrases that people like to say but don't really know much about we're gonna go through this topic and cover some great areas of knowledge you may have in the field.
Let's start with the basic question what and why convolutional neural networks there are kind of special neural network for processing data that is known to have a grid like topology this could be a one dimensional time series data which is a grid of samples over time or something like even two dimensional image data a grid of pixels in space
Convolutional neural networks have three fundamental features that reduce the number of parameters in a neural network up.
1. first we have sparse interactions between layers in typical feed-forward neural Nets. Every neuron in one layer is connected to every other in the next this leads to a large number of parameters that the network needs to learn which in turn can cause other problems well for one. Too many parameter estimates means we'll need a lot of training data convergence time also increases and we may end up with an overfit model.
CNN's can reduce the number of parameters through indirect interactions. Consider a CNN in which neuron and layer 5 is connected to three neurons in the previous layer as opposed to all the neurons. These three neurons in layer four are direct interactions for the neuron and layer five because they affect the neuron in question directly. Such neurons constitute the receptive field of the layer five neuron in question. Furthermore these layer four neurons have receptive fields of their own in the previous layer three these directly affect layer four neurons and indirectly affect a few of the layer five neurons. If the lair is run deep, we don't need every neuron to be connected to every other to carry information throughout the network. In other words, sparse interactions between layers should suffice
2. now a second advantage of CNN's is parameter sharing. This further touches on the reduced parameters as did sparse interactions before it is important to understand that CNS creates special features. Say we have an image which after passing through the convolution layer gives rise to a volume. Then a section of this volume taken through the depth will represent features of the same part of the image. Furthermore each feature in the same depth layer is generated by the same filter that convolve x' the image.
 |
| Volume in depth represents features in the same part of the image |
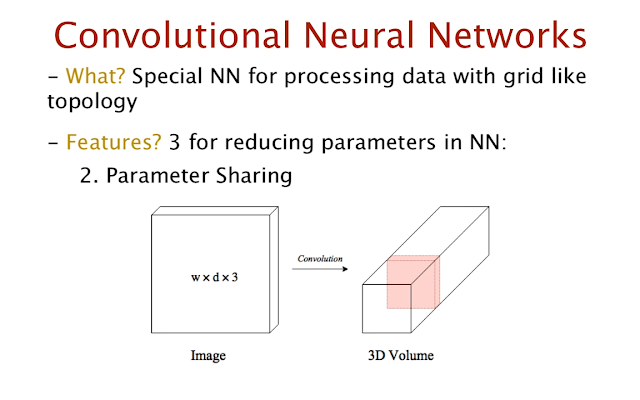 |
| Each feature in the same depth is gnerated by the same filter |
ใน 1 ความลึก ณ พื้นที่มุมหนึ่งของภาพ จะประกอบไปด้วย feature หลายๆ ฟีทเจอร์ ( N features จากแผ่น filter จำนวน N อัน) และในแนวขวาง ณ ระดับความลึกเดียวกัน แต่ละ feature ถูกสร้างจากแผ่น filter เดียวกัน
สมมติ แผ่น filter มีขนาด 11*11*3 จำนวน 96 แผ่น ดังนั้น ณ 1 ส่วนของภาพ จะมี 96 features รวมจำนวน นิวรอน ใน 1 จุดที่ทาบแผ่น filter ประกอบด้วย จำนวน weight = (11*11*3)* 96 = 34,848 จำนวน bias = 1*96 = 96 รวม 34,848+96 = 34,944 นิวรอน
The equation represents the percentage of area of the filter G that overlaps the input F at a time Tau over all time T.
f, I คือ Input และ g, h คือ filter/kernel
- สมการ 1 เปอร์เซ็นต์การ overlap ของ filter บนรูป ณ เวลา Tau จากเวลาทั้งหมด t
- สมการ 2 ใส่ขอบให้เวลาทั้งหมด
เมื่อ input และ kernel มีหลายมิติ
- สมการ 3 รูปสไลด์บน filter
- สมการ 4 filter สไลด์บนรูป *โดยทั่วไปใช้สมการนี้
ไม่ได้อ่านต่อ...
Now don't worry if this statement doesn't make any sense right now it'll be clearer when I explain more about the convolution operation for now just understand that the individual points in the same depth of the feature map that is the output 3d volume are created from the same kernel in other words they are created using the same set of shared parameters this drastically reduces the number of parameters to learn from a typical a NN another feature of convolutional neural networks is equivalent representation now a function f is set to be equivalent with respect to another function G if F of G of X is equal to G of f of X for an input X let's take an example to understand this consider that there's some image I where F is the convolution operation and G is the image translation operation convolution is equal variance with respect to translation this means that convolving the image and then translating it will relate to the same result as first translation and then convolving it now why is this used equal variance of convolution with respect to translation is used in sharing parameters across data in image data for example the first convolution layer usually focuses on edge detection however similar edges may occur throughout the image so it makes sense to represent them with the same parameters now that we understand some features of CNN's let's take a look at the types of layers we have in a convolutional neural network so we can well broadly classify this into convolution activation pooling and fully connected layers well discuss these one at a time so up first we have the convolutional layer the convolution layer is usually the first layer for CN n where we convolve the image or data in general using filters or kernels now filters are small units that we apply across the data through a sliding window the depth of the filter is the same as the input so for a color image whose RGB values gives it a depth 3 a filter of depth 3 would also be applied to it the convolution operation involves taking the element-wise product of filters in the image and then summing those values for every sliding action the output of the convolution of a 3d filter with a color image is a 2d matrix it is important to note that convolution is not only applicable to images though we can also conventional time series data I'll explain this a little more mathematically consider a one-dimensional convolution if input F and kernel G are both functions of one dimensional data like time series data then their convolution is given by this equation it looks like fancy math but it has meaning the equation represents the percentage of area of the filter G that overlaps the input F at a time tau over all time T since tau less than zero is meaningless and tau greater than T represents the value of a function in the future which we don't know we can apply tighter bounds to the integral [Music] this corresponds to a single entry in the 1d convolutional tensor that is the t f-- entry to compute the complete convolve tensor we need to iterate T over all possible values in practice we may have multi dimensional input tensors that require multi-dimensional kernel tensor in this case we consider an image input I and a kernel H whose convolution is defined as shown the first equation performs convolutions by sliding the image over the kernel and the second equation does it the other way around it slides the kernel over the image since there are usually less possible values for x and y in the kernel than in an image we use the second form for convolution the result will be a scalar value we repeat the process for every point X Y for which the convolution exists on the image these values are stored in a convolve matrix represented by I asterisk H this output constitutes a part of a feature map this is the mathematical representation of the image kernel convolution I explained before where we take the sum of products okay we got that down but let me explain it in a way that we can get a better intuition consider a number of learner Bowl filters they are small spatially with respect to the width and the height but extend deep in the first layer we convolve every filter with the image so this means it slides along the image and outputs the convolve to deactivation or feature map note that the depth of the filter is equal to the depth of the volume in the case of a first layer of convolution where we're dealing with an input image of depth 3 then we'll also have a filter of well X cross X cross 3 and by the way the three for the input image is because of the RG and B channels I'll give you a better example here consider the Emnes dataset with 60,000 28 cross 28 images if we perform 2d convolutions with a 3 cross 3 filter and its ride of one stride being the amount that we want to move the sliding window after every convolution then we'll end up with the feature map of size well 28 minus 3 plus 1 which is 26 across 26 now if we apply say 32 such filters on the image then we'll end up with 32 such 26 26 feature maps these are stacked along their depths to create an output volume in this case of size 26 cross 26 cross 32 this will be the feature map I mentioned earlier so what do these pixels in the output represent the top left corner with its depth 1 Cross 1 cross 32 each of these 32 numbers corresponds to different features of the same 3 cross 3 section of the original image these features are dictated by the kernel or filters using convolution some can be structured to find curves others to find sharp edges others for texture and so on in reality some or most of the features that are used especially that are in the deeper layers of a convolutional network are not interpretable by humans there is much more to this but I will link several resources down in the description below I strongly recommend the chapter on convolutional neural networks in the deep learning book by Ian good fellow for now I think I've spoken enough about convolution so I'll move on to the next layer the activation layer only nonlinear activation functions are used between subsequent convolutional layers this is because there won't be any learning if we just use linear activation functions so what do I mean by that let's consider a 1 and a 2 be two subsequent convolutional filters applied on X without a nonlinear activation between because of the associativity property of convolution these two layers are effective as just a single layer the same holds true for typical artificial neural networks ten layers of a typical a NN without activation functions is effective as just having a single layer typically we use Li kirei Lu instead of the rail activation in order to avoid dead neurons and the dying Rayleigh problem note that the activation isn't necessarily executed after convolution many papers follow the convolution poling activation order but this isn't strictly the case let's take a look at the next layer that I just mentioned pooling pooling involves a down sampling of features so that we need to learn less parameters during training typically there are two hyper parameters introduced with the pooling layer the first is the dimensions of the spatial extent which in other words the value of n for which we can take an N cross and feature representation and map to a single value and the second is the stride which is how many features the sliding window skips along the width and height which is similar to that what we saw in convolution a common pooling layer uses a 2 cross 2 max filter with the stride of 2 this is a non overlapping filter a max filter returns the maximum value among the features in the regions average filters which return the average of features in the region can also be used but the max pooling works better in practice since pooling is applied through every layer in the 3d volume the depth of the feature map after pooling will remain unchanged performing pooling reduces the chances of overfitting as there are less parameters consider the Emnes dataset after the output from the convolution layer that I discussed previously we have 26 across 26 across 32 volume that's great now using a max pool air with 2 cross 2 filters and astride of to this volume is now reduced to a 13 cross 13 cross 32 feature map clearly we reduce the number of features to 25% of the original number this is a significant decrease in the number of parameters okay now we're going to talk about converting it to a fully connected layer so here's a question what exactly is the use of fully connected layers the output from the convolutional layers represents high level features in data while that output could be flattened and connected to the output layer adding a fully connected layer is usually a cheap way of learning nonlinear combinations of these features essentially the convolutional layers are providing a meaningful low dimensional and somewhat invariant feature space and the fully connected layer is learning a possibly nonlinear function in that space so how do we convert the output of a pooling layer to an input for the fully connected layers well the output of a pooling layer is a 3d feature map a 3d volume of features however the input to a simple fully connected feed-forward neural network is a one dimensional feature vector for the 3d volume they are usually very deep at this point because of the increased number of kernels that are introduced at every convolutional layer I say every convolutional layer because while convolution activation and pooling layers can occur at many times before the fully connected layers and hence is the reason for the increased depth to convert this 3d volume into one dimension we want the output width and height to be 1 this is done by flattening this 3d layer into a 1d vector consider our Emnes dataset again where the output feature map is 13 cross 13 cross 32 by flattening our 13 cross 13 cross 32 volume we end up with the vector of 13 times 13 times 32 cross 1 or 5400 8 cross 1 that is a 5400 a dimensional vector which is in an admissible form for the fully connected layers from here we can proceed as we would for fully connected layers for classification problems this involves introducing hidden layers and applying a softmax activation to the last layer of neurons now that we got all the theory down let's take a look at CNN structure for the complete and Miss dataset we initially start with 28 cross 20 images grayscale images the image is passed through a convolutional layer here we apply 32 3 cross 3 filters note that the depth of the filters is the same as that of the input which is 1 in this case 4 very scaled images the output of convolution with respect to each filter is the width of the image - width of the filter plus 1/4 a stride of 1 the same form applies to the height so the output has a width and height of 28 minus 3 plus 1 which is 26 since the depth is equal to the number of filters the output of convolution is a 3d volume of dimensions 26 cross 26 cross 32 we can then say pass this into a ray Lew or leaky ray low activation function in order to get an intermediate feature map activation now it doesn't change the dimension spatially so we still have a 26 cross 26 cross 32 volume after activation we can pass this into a max pooling layer with 2 cross 2 filters in a stride of 2 such a non-overlapping pooling layer is a common design choice in chaos we can pass a padding parameter while pooling it takes two values the first is either valid which means that there's no padding so that we don't slide the kernel off the borders of the image and the second is the same in which we pad the input such that the pooling layers can cover the entire image let's consider a valid pooling where the output width is equal to the input width - with the filter + 1 / stride so output width is equal to 26 - 2 + 1 divided by 2 which is 13.5 but the value is floor - 13 as we don't introduce padded pixels the output height is the same and the depth remains unchanged this leads to an output volume of 13 cross 13 cross 32 after this say we perform another round of convolution activation and pulling for convolution for example let's consider some 64 filters of 3 cross 3 in this case the output would be 11 cross 11 cross 64 why because the output is equal to the input width minus the filter width plus 1/4 convolution of strike 1 that's 13 minus 2 plus 1 and the depth is equal to the number of filters which is 64 we can pass this through an activation layer that doesn't really change its dimensions for the next max pooling layer the size is reduced to 5 cross 5 cross 64 as the output width and height is 11 minus 2 plus 1 divided by 2 which is 5 and the depth is preserved we can now feed the output of this polling layer to a fully connected layer by flattening it to one dimension so we have 1600 input features over our a n n we can then connect it to a hidden layer of say 512 neurons and then apply dropout and output it to a soft max layer of 10 neurons would signify the probability of being the digits 0 through 9 and so we have a full-fledged convolutional neural network CN NS are being used everywhere for example to generate data like image audio or text in generative adversarial networks the generator is modeled as a convolutional neural network they're also using gameplay like go and Atari games through deep cue learning which combines CN NS with cue learning and reinforcement learning in the field of medicine they are used in medical imaging from the segmentation of knee cartilage to the detection of Alzheimer's disease in MRIs clearly there's a lot of potential for CN NS in various fields I've included links to interesting blogs and papers about CN NS in the description down below hope you guys understood more about the nature behind convolutional neural networks it's not magic and every component has its purpose give the video a thumbs up and hit that subscribe button for more awesome content and I will see you in the next one bye bye
Sign up here with your email


ConversionConversion EmoticonEmoticon